IDCC-I: Poster Session
Poster: Three approaches to grade diamond cut: parametrical, direct light measurements, and 3D model
Poster: Introducing a set of Basic Light Responses (BLR) and building a cut grading system based on these (clusterization)
Poster: The importance of the relationship between the pupil of a human eye, a light source, and the size of diamonds virtual facet
Poster: How symmetry affects diamond appearance: mutual relationship between diamond proportions and symmetry
Poster: Three approaches to grade diamond cut: parametrical, direct light measurements, and 3D model
Three different approaches are now used for grading the cut quality of a diamond. The first is based on analyzing the set of cut parameters (proportions and angles). The second involves instrumental detection of the light returned by the diamond. The third is based on 3D modeling of the diamond. Below, we analyze the advantages, drawbacks, and limitations of the above-mentioned approaches.
1. Parameter-based description of a diamond.
Two principal problems arise when using this approach. First, the parameter set presently used in laboratories describes an ideally symmetric diamond and, therefore, does not completely describe the shape of a real diamond. Moreover, this parameter set does not completely describe even a symmetric stone, because it does not include the coordinates (angles and azimuth) of the upper and lower girdle facets. The second problem is that different cut parameters of a diamond are interdependent in the sense of their combined influence on the optical effects demonstrated by the stone. In the existing gemological grading systems, the cut parameters are usually considered as independent. Therefore, the zone of high-quality diamonds, plotted in the "crown angle - pavilion angle" coordinates, looks like a rectangle. However, it is known that such parameters as the crown and the pavilion angle are interdependent. Therefore, it is easy to find such combinations of the parameters, which conflict with the conventional grading. Cutting diamonds with different combinations of the crown and pavilion angles would allow one to draw a corrected "quality map". However, all the other cut parameters should be fixed in such a case. This means that the corrected "map" will not be valid for a stone with a deviation in any of these parameters (for example, in the table size, star facet length, lower girdle facet length, or upper girdle facet azimuth). Considering each extra parameter leads to exponential growth of the possible cases, and the problem of building a parameter-based database that describes all these cases becomes more and more complicated, and even unsolvable (starting from a certain number of the considered parameters, which yields an enormously large number of cases to classify). Therefore, when the parametric approach is used in practice, some of these parameters are anyway fixed (their influence on the stone appearance is deliberately neglected). However, this influence does actually exist. As a result, this fixing leads to building such a cut grading system that sometimes conflicts with real cases. It is clear that the above-discussed limitation is fundamental for the parametric approach (database approach).
For example, the results of recent diamond cut studies carried out at GIA show that "every facet matters". Probably, the GIA grading system does not reproduce the errors peculiar to the "quality rectangle" approach. However, similar errors may occur due to neglecting some other cut parameters. This is a direct consequence of the fact that the GIA system, though considering slightly more parameters with respect to the preceding systems, still employs the same approach. The approach remains parametric.
.gif)
Figure 1
The problem of taking into account the interdependent parameters is illustrated in Fig. 1. The left end of the segment corresponds to the situation when all the parameters are independent (which does not reflect the actual state of things). The right end of the segment corresponds to the situation when all the parameters are considered along with their interdependence (such a database is almost impossible to construct, due to an enormously large number of cases to classify). The dots correspond to the grading systems developed in different laboratories, such as AGS, HRD, and GIA.
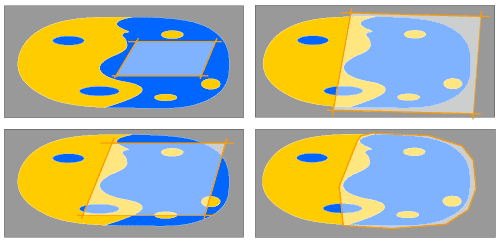
Figure 2
2. Cut grading based on optical measurements.
Examples of instruments that use the second approach are the Brilliancescope, Firescope, Hearts and Arrows Viewer, Idealscope, and Isse-2. The design of these devices is based on the use of fixed types of structural illumination. If it's a priori known that some stone is "good", it is always possible to choose such an illumination type, for which this stone will be clearly distinguishable from the others. As a result, such a device will check how the diamond under study is close to (or far from) the initial etalon (which is usually called a Masterstone). All these instruments allow one to reject those stones looking different from the Masterstone. So, all such stones will be graded as "bad", even if some of them look quite good when viewed by the observer.
It is important to understand the difference between the method of looking for bad stones and the method of looking for good stones (see Fig. 2).
3. Cut grading based on 3D modeling.
An accurate 3D model of a diamond completely describes the shape of the stone and allows one to synthesize photorealistic images of the stone under different lighting conditions and to calculate the individual optical coefficients for every stone. A cut grading system can be built on the basis of the 3D model. On this way, it is important to adequately model the illumination, the diamond, and the observer, as well as to properly choose the coefficients to compute. The main drawback of this approach is the need for system verification using real diamonds (including those having non-standard cut proportions) supplemented with expert grading data for these stones. However, it is worth noting that this drawback is peculiar to all the approaches considered.
Poster: Introducing a set of Basic Light Responses (BLR) and building a cut grading system based on these (clusterization)
3D diamond model can be used as a base for cut grading system development. Various light responses of this model can be calculated. This computation involves transition from metric (angular) parameters to optical ones.
Examples of such light responses are light return to the observer's eye, light leakage though the pavilion, "nail head", ETAS, and others. For this response set, we have introduced the acronym BLR (Basic Light Responses). The value of each of the responses can be computed on the basis of the 3D model of the diamond. This value is individual for every diamond and characterizes its cut. In our opinion, three types of such responses should be considered. The first type involves those responses directly perceived by the observer, that is, scintillation, brilliance, fire, and contrast (all these responses are graded as positive). The second type involves those responses graded as negative by the observer. These are "fish-eye", "nail head", and light leakage. The third type involves those coefficients characterizing the cut, regardless of the lighting and viewing conditions, for example - ETAS. So, the set of BLR coefficients can be redundant with respect to the set of visually observable properties.
The next step is dividing the Diamond Cut Masterset into groups, in accordance with the BLR values computed. Independently of this, experts divide the diamonds into groups on the basis of the human grade of the diamond beauty and its components, such as brilliance, scintillation, fire, and contrast. Thus, two independent grade arrays (clusters) arise: a computation-based cluster and an expertise-based cluster.
A special method based on neural network principles allows one to compare the two data arrays and to build a diamond grading system. The comparison of the BLR-based grades and experts' grades may lead to one of the two possible situations.
1. The BLR dataset is enough to predict the human visual grade, and, therefore, the cut grading system is built.
2. The BLR dataset is not enough to divide the diamonds into groups introduced by the experts. In such a case, to complete the cut grading system, it is necessary to analyze those diamond groups discriminated by the experts, but not discriminated by the computer, to find the light response accountable for this discrimination, and to add it to the BLR set. After that, the BLR set will become enough to perform cut grading.
The approach described above is robust against non-essential errors both in the diamond expertise and in the BLR computation.
Poster: The importance of the relationship between the pupil of a human eye, a light source, and the size of diamonds virtual facet
A common flaw in most ray tracing software modeling approach is to consider the eye as a tiny point aperture, and light as discrete rays.
The virtual facets of a diamond are like windows and mirrors that allow you to see into parts of the space surrounding a diamond. A crown facet may split into a dozen virtual facets by the pavilion facets below. The pupil of a human eye is not a virtual pin hole, it has a diameter which increases the parts of space that we might see through each of these virtual facets.
Any bright lights that appear in this additional part of space will be visible to a human eye as a sparkle. This sparkle is not be predicted by most modeling software. DiamCalc also adjusts the pupil aperture when considering different lighting environments, just as our eyes do naturally and additionally assumes that viewers have two eyes, not one. Two eyes almost always see more sparkle and fire than one.
Diaphragm (hole or virtual facet) D in Fig. 3 allows a light source to be visible inside a cone. This models a simple diamond with only one large virtual facet.
.gif)
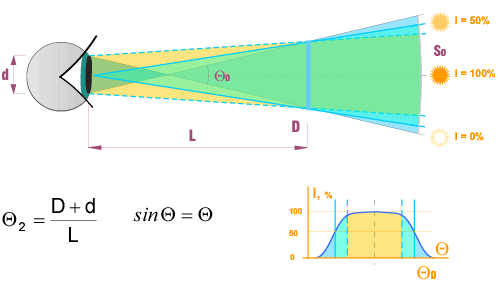
Fig. 3 The light source is in focus.
If we divide this diaphragm into two facets, D1 and D2, that have the same total area and then separate them in space the total visible space increases: S1+S2>S0
Brightness of light on the image side. At the retina an image can be dimmed and its brightness will be less.
The diaphragm fragmentation and the diaphragm fragment rotation. This is how a diamond works with light, increasing a part of visible space and so gaining more potential to sparkle.
Because a well cut diamond also acts as mirrors as well as windows, it also changes the direction of light, just like a mirror. ETAS (effective total angular size) is a part of all the space that we can see through a diamond.
An observer sees light in a diamond if a light source is placed within any cone coming to our eye through a diamond. All these cones form part of space calculated as ETAS. This shows how all these cones are placed on a sphere (green is light emitted form the crown, red is from the pavilion and yellow has come from the girdle. Blue has hit into the observer's head).
The effectiveness of a diamonds beauty depends on the quantity and size of virtual facets created by its cut, and on the distribution of the cones of vision (ETAS) created by its virtual facets. It is important that a diamond redirect light from neighboring parts (virtual facets) to quite different parts of space. This way an observer can see light in many parts of space. These three images of alternating brightness and darkness (shown simply as black and white squares) show how the angular size, or the cones of the virtual facets, relates to the size of bright and dark areas in the space around the diamond.
White squares represent parts of space that allow for light sourse to be visible. In Fig. 6a the size of the black-white areas are too large: very few parts of space and some light sources are not visible. The white areas have an optimal size for balance between the quantity and the size of light cones: all light sources are visible.
Increasing the quantity of virtual facets results in a decrease in their size. Because of this the amount of light coming to your eye is too small and is not perceived as a bright sparkle; i.e. the brightness is comparable with the background.
Poster: How symmetry affects diamond appearance: mutual relationship between diamond proportions and symmetry
How asymmetry relates with proportions in their mutual influence on diamond appearance and beauty?
The proper proportions of diamond can maximize its optic appearance: scintillation, brilliance and fire. Deviations of cut proportions can create some undesirable effects of diamond appearance, and sometimes require compensation by deviation of other corresponding proportions and angles.
In this poster we discuss a possibility of improving diamond optical appearance by some symmetry deviations. The problem is that today any symmetry deviation visible by loupe penalizes diamond cut quality by definition.
A general observation reveals that an overall diamond picture (pattern, appearance) is created by facet arrangement. Proportions and symmetry here are two sides of one coin. The following example illustrates relationship between deviations of proportions and deviations of symmetry.
Various symmetry distortions are connected with the number and shape of diamond virtual facets that are critical for scintillation. If a bigger stone has exactly the same shape and symmetry it will have the same number of virtual facets but with bigger size. Probably it is better to implement some special symmetry distortions in order to achieve more virtual facets and more scintillating diamond.
It is important to separate asymmetry of diamond shape (visual) and asymmetry of facet positions.
What is better: to distort symmetry in order to avoid some negative optical effects due to improper proportions or leave a stone with improper proportions and perfect symmetry?
