On the problem of grading the quality of diamond cut: an analysis of some aspects of the problem

Introduction

This article is devoted to the study of diamond cut. Application of computer modeling technologies to studying diamond cut and developing a cut grading technique is demonstrated. To build an effective cut grading system one must not only model correctly the diamond under study, but also the illumination and the observer. Conditions of observing white and colored rays in light passed through a diamond are analyzed. The diamond is considered as an object that produces inhomogeneities in the spatial distribution of light. We also discuss how to proceed from analyzing model diamonds to grading the cut of real stones .
The article is directed to specialists on cut issues rather than a guide to consumers in the process of buying a diamond right now. It contains some considerations about the future practical value of a cut study grading system being developed.

We use a language such as facets, prisms, ray paths, mirrors, reflections, and so on. This language is useful for understanding and explaining various phenomena, and many researches uses this language when analyzing and quantitatively describing different phenomena in relation of diamond appearance.

In posting this material we wish to bring attention to the importance of understanding appropriate illuminating and viewing conditions, and we aim to stimulate collaboration toward a standardization of observation conditions for evaluation of diamond appearance.

Recent achievements

If it's time to learn how to grade diamond cut and how to distinguish between good and bad diamonds (from the viewpoint of their cut quality), we can suggest an appropriate method (technology, approach). At the initial stage of our research we have studied of appearance of ideal symmetry diamond models:

The Results of Diamond Cut Studies Carried out in MSU, 1999

and at the second stage we have posted our approach to nonsymmetrical diamonds in September 2000:

Developing of Diamond Cut Grading System by MSU (OctoNus and GC MSU) Computer Tools

Important events regarding our approach have occurred since that time.

A. OctoNus have developed software allowing you to visually analyze the appearance of a diamond and to quantitatively estimate some features of its cut, such as Light Return, Light Leakage, Fish Eye and Contrast, based on a diamond 3D model.

B. Sarin Technologies have developed a method to build a 'solid' 3D model of a scanned diamond. Many users worldwide are now able to create models of real stones and exchange these models via Internet.

C. OctoNus software enables the Sarin 3D model to be 'viewed' and tested without the diamond being present.

D. As a result of these developments it is now possible to develop a system for grading the quality of diamond cut of any individually scanned diamond using 'basic light responses' (BLR) of the diamond in conjunction with formalized criteria established by experts. This means an expert cut quality assessment system is now feasible that could be applied to any diamond irrespective of its shape or symmetry.

Building of cut grading system

In the present material, we would like to advance the following assertions:

Assertion 1. Diamond cut grading should be based not on measured geometric parameters (a parametric model of the diamond). Another approach, based on analyzing the complete 3D model of the diamond, is much more effective.

Image generated by the GemAdviser software on the basis of a 3D model of a real diamond, which was obtained by Garry Holloway with a Sarin machine.	The same diamond in the face-up position, as viewed through an IdealScope. Photo by Garry Holloway, www.ideal-scope.com

This analysis can be done by means of computer modeling.

Only symmetric stones can be effectively graded on the basis of the geometric parameters. An attempt to correctly grade an asymmetric stone using this approach would face at least two problems.

Namely:

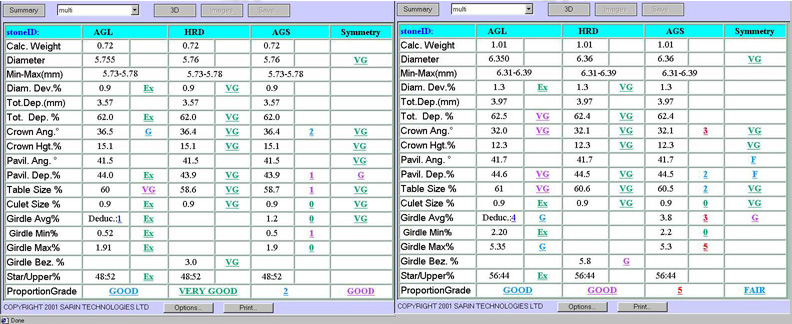
1.1 Taking into account various deviations of the diamond geometry from the perfectly symmetric leads to the necessity of introducing more and more parameters. To correctly describe all these deviations, a very large number of parameters (such as 100 or 200) may be required. To make the grading procedure correct, the interrelation between all these parameters should be analyzed. Otherwise, some negative consequences may arise. This can be shown using the AGS system as an example.

Work with scanned diamond models

Click on any diamond picture below to download corresponding GemAdviser model. Once model is opened by GemAdviser software we also recommend you to click on green "play" button to see this virtual diamond in motion.

Model AGS2	Model AGS3
Launch interactive model	Launch interactive model

Sarin Reports	The distribution of the cut quality function Q with AGS grade.

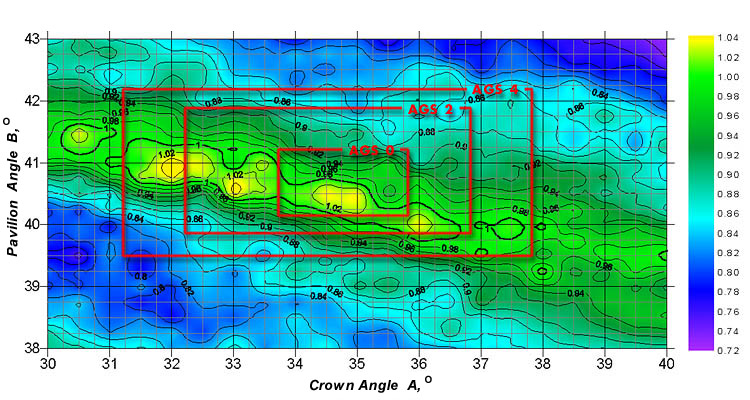This system grades each of the cut parameters independently and cannot grade even such evident correlations as that between the crown angles and the pavilion angles. The analyses of these correlations is very complicated if the number of the parameters is about 10 and almost impossible if this number is about 100.

Example with tilted table

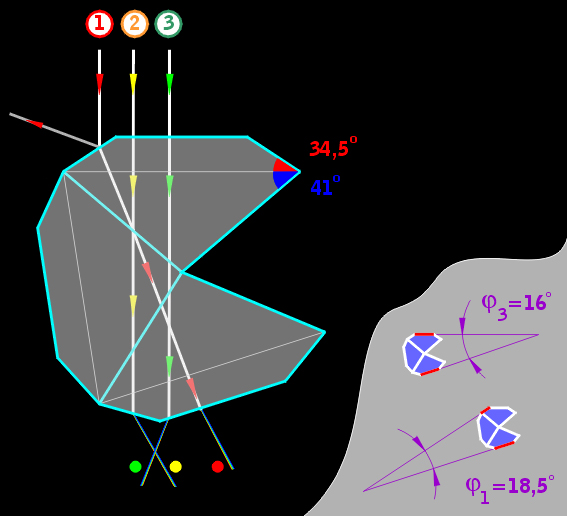
The inclination of each diamond facet should be correctly defined. In other words, a plane should be defined, relative to which the inclination is measured. For instance let us consider a diamond with one symmetry deviation - inclination of table plane on 1 degree.

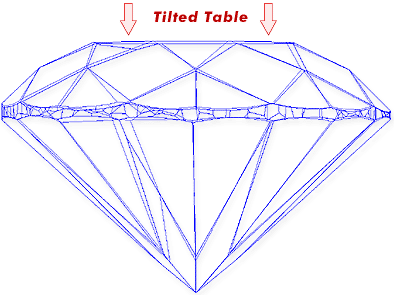
Registered DiamCalc users can download this model and see it as wire-frame model.
Click here to download "TiltedTable.dmc"

To check whether the girdle plane is parallel to the table plane, gemologists got used to examining the stone from the side with a loupe. However, this way allows one to notice possible non-parallelism only if it is strong enough. For instance, an expert equipped only with a loupe would hardly notice a table tilt of 1 degree, as in our example. So, the expert would grade the stone as good, in the sense of the symmetry distortion considered. Should one put the stone into a scanner in the table-down position, scan it, and measure the angles in the model, the stone will appear to be bad, because the scatter of the facet angles amounts now to 2 degrees.

Measuring the cut parameters with a Sarin machine yields a large scatter of facet inclination angles (from 34.2 to 35.6 degrees for the crown facets; from 40.8 to 42.6 degrees for the pavilion ones. Due to this scatter, the existing grading systems would grade such a stone as bad. However, the angles are actually all right, the only problem being the inclined table. Therefore, the stone looks quite good, shows enough brilliance and fire, and is decently graded by the GemAdviser software. Those readers having the registered DiamCalc product are able to work with the draft (wireframe or facet junction) model of this stone and to check the inclination angles for each crown and pavilion facet.

Click here to download "TiltedTable.dmc"

The appearance of this stone strongly differs from that of stones with all pavilion facet angles equal to 40.8 or 42.6 degrees, but is similar to that of a stone with all pavilion facet angles equal to 41.7 degrees. In order to obtain your own opinion you can go to links below and to compare you visual estimations with GemAdviser scores.

Click on any picture below to download corresponding GemAdviser model. Once model is opened by GemAdviser software we also recommend you to click on green "play" button to see this virtual diamond in motion.

Pavilion angle 40.8 Crown angle 34.2	Pavilion angle 42.6 Crown angle 35.6
Launch interactive model	Launch interactive model
Scanned diamond	Pavilion angle 41.7 Crown angle 35
Launch interactive model	Launch interactive model

We can see that a more accurate method for determining and communicating crown and pavilion angles is required. A more correct definition of the pavilion angle is the angle calculated on the base of angle between opposite facets and this reduces the additive error of symmetry distortion with the existing cut grading systems. Therefore our stone has only a very slight symmetry distortion and appears as a stone with a crown angle of 35 degree and pavilion angle of 41.7. However other symmetry distortions exist that this approach will not solve or diminish so it is better to work with a complete 3D model of the stone rather than with a set of its parameters.

BLResponses

Assertion 2. It is expedient to split diamond grading into two stages.

At the first stage, a basis of a complete or redundant BLResponses system is being built: a computer works with a model, calculating its BLResponses, such as Light Return, Light Leakage, Fish Eye and Contrast. Standardized conditions of lighting and viewing are used for this purpose.

At the second stage, the complete or redundant BLResponses system is used to grade the stone on the basis of formalized experience of experts. The experts' knowledge determines preferences of different groups of customers.

Assertion 3. To complete the above-mentioned tasks, it's necessary to use adequate models of illumination, diamond, and observer. The latter means that psychophysiological properties of human perception should be taken into account. Inadequate modeling of any of these objects may lead to fundamentally erroneous results. To prove this statement, we would like to consider studies performed at GIA. They use methods similar to ours, but obtain essentially different results.

Analysis of illumination

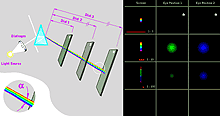
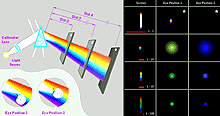
Analysis of different models of illumination

	Fig.1. One white-light ray originating from an illumination source. Angle of prism 37°
	Fig.2. Parallel rays emitted by an illumination source. This scheme can be realized either by moving a point source to infinity or by using a collimating lens. Angle of prism 37°
	Fig.3. Real illumination source. A source emits rays that diverge within the angle Q=6°. Angle of prism 37°
	Fig.4. Real illumination source. Q=0.5°. Angle of prism 16° corresponds to angles of Tolkowsky cut.
	Fig.5. Representation of diamond as a set of prisms.

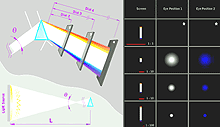
Demonstration of adequacy of illumination model no. 3

Photographs of real stones confirm that the illumination model corresponding to Fig.3 is adequate, while the two simplified models (Fig. 1 and Fig.2 ) are inadequate:

1. Dark area	2. Blue color	3. Light blue color
4. White area	5. White area	6. White area
7. Yellow color	8. Brown color	9. Dark area

All these pictures are taken on the same conditions with the diamond is rotated with step of one degree around vertical axe. It was illuminated with a big angular size light source. Authors understand that rotating a diamond is not the same as rotating a camera. But there was no possibility to rotate the camera.

To better understand sections 3.3, 3.4, 3.5, and 4, it is recommended to read the following papers published in Gems&Gemology journal:

For section 3.3 - "Modeling the Appearance of the Round Brilliant Cut Diamond: An Analysis of Fire, and More About Brilliance", Gems&Gemology, Fall 2001, Vol. XXXVII, pp. 174-197 (pay attention to the DCLR formula on page 183).

For sections 3.4 & 3.5 - "Modeling the Appearance of the Round Brilliant Cut Diamond: An Analysis of Brilliance", Gems&Gemology, Fall 1998, Vol. XXXIV, No. 3, pp. 158-183.

GIA's illumination model: Main consequences of GIA's illumination model

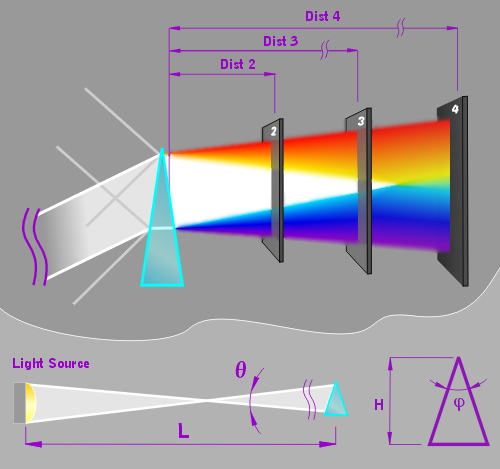
To study the fire of a diamond, the GIA group uses an infinitely distant point source, just the same configuration as that shown in Fig. 2. In such a model, a light beam passed through a prism consists of only colored rays at an infinite distance from the prism.

Therefore:

In the GIA model, the probability of observing a green ray is the same as that for any other color. In real diamonds, green rays are observed much more rarely than blue and yellow rays;

GIA metric for dispersed color light return DCLR is almost independent of dispersion. For example, if we consider a material, the dispersion of which is two times weaker than that of diamond, the DCLR will be almost the same as that for diamond! Moreover, if we suppose that there is absolutely no dispersion in the material of the considered stone, the DCLR not only fails to become zero, but even remains close to the value calculated by GIA (just dispersion, not refractive index). Let us consider green color, which is located in the center of visual color range and red and blue colors lie on opposite sides of the green color, at equal distances on visual spectrum. The deviation of blue and red spots from green spot on registration sphere depends on the dispersion of the material. In any case, these deviations are small enough and almost equal one another. Note

When calculating DCLR, the GIA team performs summation. As a result, the red and blue rays compensate each other, and their overall mean DCLR is almost equal to that of the central green ray. Then let us change (decrease) dispersion value of material fixing refractive index for green color. The location of all such green spots on the sphere used by the GIA group for registration will not change, and blue and red spots will be closer to green. When calculating DCLR blue and red rays again compensate each other and we will get the same DCLR value as before!

This statement can be illustrated by the following formula:

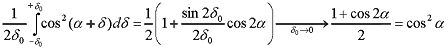
Here for each arbitrary light beam:
a - direction of green ray
2d - angle between red and violet rays.

It is clear from the common sense that if dispersion equal zero fire will not appear. Thus, the following questions arise: What is the merit of the GIA's approach from the viewpoint of modeling the fire and what does the DCLR metric actually describe?

Important notes :

1. Actually blue ray can be located further from green than red ray, especially when rays refract from diamond at the angle close to critical. It does not influence on DCLR, however it influences on picture really observed. This is one reason why we observe blue color more often that red, and why most frequently observable colors in diamond viewed at close distance - blue and yellow. Here authors consider angles near critical and smaller it on 2-3 degrees (for example range from 16 up to 21 degrees.) At the large angles the refraction losses are sharply increased, and also the beam area changes, that results in sharp loss of intensity and decreasing of possibility to observe any color.

2. The second reason why more often we can see blue and yellow colors when look at diamond from close distance or use photo camera ("Macro" mode) is color mixture properties. Taking range of spectrum from blue to green and adding green color a little we will get cyan color as a mixture. The range of spectrum from red to green with addition of the same little amount of green will be mixed into orange. Under real not very bright illumination conditions a human vision will see cyan as blue color, and orange as yellow or brown color, not as red.

We have just shown that the DCLR takes into account fire that does not actually exist. It is also important to show that the DCLR does no take into account fire that does actually exist. The problem is that the GIA's illumination source produces only one type of rays, namely, those rays normally incident on the table of the diamond. In reality, a ray may be incident on the diamond at any angle. As far as we know, observers usually grade a diamond, holding it in the face-up position. In this case, the fire they observe originates from light incident not normally to the table plane (typical range of incidence angles is 10-15 degrees, with respect to the table normal). Anyone who has a diamond, may observe the fire phenomenon with a source that obliquely illuminates the table of the diamond. Thus, the DCLR coefficient does not take into account a considerable portion of the actual fire, maybe the most of it. This is also due to the fact that the illumination model is inadequate.

As it can be seen, the results obtained by the GIA group contradict practice. The inadequacy of the illumination model is the main reason of this contradiction. A real light source emits rays in all directions.

Therefore, not parallel but diverging rays enter the prism (see Fig.3 Click to see figure 3). If the dispersion angle of the material of the prism is less than the divergence angle of the incident light, there are some white rays at any distance from the prism. Moreover, in the most of real cases, the white rays prevail over the colored.

Therefore, in practice green rays are observed rarely, and when the dispersion decreases, colored rays disappear, leaving only white-light beam to observe.

"Brill" software analyses light response

Let us consider the ratio between white and color light using the software "Brill":

	An infinitely distant light source, such as that used at GIA to analyze fire, which produces parallel rays, creates mainly colored highlights on a screen placed at a distance of 75 mm (the hemisphere radius) from the illuminated diamond. When this distance is longer, white highlights can be produced only by those rays reflecting off the surface of the diamond and not entering it. All the refracted rays are observed as colored.
	The position of the screen is the same (75 mm from the diamond), while the light source now has a finite angular size (3 degrees). The highlights produced in this case consist of both white and colored portions. It can be seen that the white ones prevail.
	The distance between the screen and the diamond is increased to 0.5 m. One can still observe both white and colored portions in the highlight pattern, the white ones still prevailing. The angular size of the light source is 3 degrees, as before.
	To get rid of white highlights, it is necessary to decrease the angular size of the light source. In this example, the screen-to-diamond distance is 0.5 m and the source size is 0.5 degrees. Only colored highlights are observed on the screen, however their area is small.

Basing on the figures presented and the results yielded by the modeling software, a careful reader may notice that the amount of fire or, more precisely, the overall area of colored highlights is not maximal for a light source with a small angular size. Increasing the angular size causes not only the appearance and intensification of white highlights and the decay of green ones, but also an increase in the overall area of blue and red highlights. So, the optimum angular size of the source can be neither too small nor too large.

WLR metric and brilliance

Analyses of correlation WLR metric and brilliance
See "Modeling the Appearance of the Round Brilliant Cut Diamond: An Analysis of Brilliance", Gems&Gemology, Fall 1998, Vol. 34 No. 3, pp. 158-183.

Other authors have already noted many times that the GIA illumination model (illumination source; the absence of observer's profile) is inadequate for calculating the WLR coefficient. We agree with this criticism, but wish to point out an error in the GIA approach, which is more serious than it was reported by these authors. Our opinion is that the WLR coefficient will not correlate with the brilliance even if one corrects the illumination model. The error is wrong understanding of what is the brilliance of a diamond.

First, GIA identifies the brilliance with light return.

Second, the light return is determined as the light returned from the diamond into the upper hemisphere.

Without any explanation, GIA excludes any external luster when defining the light return. However, we treat this as a technical problem of GIA and further include the external luster in the definition of the light return). Further, we will use the abbreviation LRGIA to denote the total light return into the upper hemisphere, while the abbreviation LRMSU will be used to denote the light reaching the observer's eye (eyes, for a stereo-observer).

We would like to stress that we identify none of these two figures with the brilliance. The above ideas are easier to comprehend if you imagine a mirrored disco ball. It produces a lot of reflections on the walls, ceiling and floor, but a person sees just a few at once.

Example with mirrors

We will now try to explain why the above error is the most serious of GIA's mistakes and to follow the consequences of this error, using a rather simple example. Consider the following system:
In its left window, the Brill software models a single mirror that swings in such a way that the mirror inclination ranges from zero to 3 degrees. You may observe the source image motion caused by this swing. One complete highlight is permanently seen while the mirror swings.

- Square mirror with a size of 35x35 cm;

- Observer at a distance of 60 cm from the mirror, the pupil diameter of the observer's eye being 4 mm;

- One small (point-like) incandescent lamp placed at a distance of 2 m from the mirror.

Let us adjust the mirror so as to make the observer see the lamp approximately in the center of the mirror. When the mirror is viewed from the point where the lamp is located, the angular size of the mirror is about 10°, while the observer would estimate the angular size of the mirror as 32°. If we consider a light beam that originates from the lamp, reflects off the mirror, and finally enters the pupil of the observer's eye, the diameter of this beam measured in the mirror plane will be 3 mm.

Let us now analyze the light reflected by the mirror (the coefficient LRGIA) and the light entering the observer's eye (the coefficient LRMSU). We shall use the abbreviation LRGIA0 to denote the coefficient LRGIA calculated for the specific position of the lamp and the abbreviation BR0 to denote the mirror brilliance for this case.

Now suppose that we have split the mirror into 100 equal portions (for example, squares) and randomly tilted each portion by an angle that ranges from -3° to +3°.

Now the software models splitting the original mirror into 100 portions (10x10). Each of the portions is randomly tilted by an angle ranging from zero to 2 degrees. As before, the whole object swings with an amplitude of 3 degrees. In this case, the number of highlights visible at once ranges from zero to a few ones. Some of the highlights are complete, while other are just fragments.

Let us calculate LR_GIA, WLRGIA, LRMSU, and the brilliance BR, for this new object. Since the angular size of the original mirror is small, LRGIA will remain almost the same, slightly fluctuating around LRGIA0. (Since GIA weighs the light return using COS*COS function, a weighted coefficient, WLRGIA may slightly change with respect to WLRGIA0 and fluctuate, depending on the distribution of the tilt angles of the mirror portions.

Probably, one of the main purposes of introducing the weighing procedure was the necessity of some non-negligible variations of LRGIA. In fact, the coefficient WLRGIA is a measure of the spatial distribution of the reflected light. As for the observer, he will see a certain number of lamp reflections. The minimum possible number is 0. The maximum equal to 100 is achieved in the case when each mirror portion reflects light towards the observer's eye. All the lamp reflections will be as bright as the single reflection visible before the mirror was split. The actual number of these reflections depends on the tilt angles of the mirror portions and the positions of the lamp and the eye.

(If the observer views the mirror with two eyes, the number of visible reflections fluctuates within the same limits, but the average number will be two times as large as that in the case of single-eye viewing. This is because each reflection could be detected by either the right or the left eye, which are spatially separated. When your eyes see the two spots on the flat mirror your brain merges them into one spot. But when you look at two mirrors and each eye sees one reflection in each mirror the brain will perceive two reflections).

You will probably agree that the brilliance (BR) substantially depends on the number of simultaneously viewed reflections. The larger this number, the more brilliant the mirror looks.

To a first approximation, we can assume that the BR coefficient is proportional to the number of visible reflections. (Here we use the fact that all the reflections have the same brightness). Accordingly, BR will randomly oscillate in the range from 0 to 100 BR0 (the expectancy of this function depends on many parameters, in particular, on the distribution function of the tilt angles of the mirror portions). This is easier to comprehend if you again imagine a mirrored disco ball. In any specific case, you would see a few lamps, the brightness of each lamp coinciding with that of the single reflection visible before the mirror was split.

The software calculates the coefficients LRGIA, WLRGIA, and LRMSU, the left column containing their current values. As for the right column, it contains the mean values of the coefficients, averaged over the time passed since the software was started or the Refresh button was pressed. You may vary the maximum tilt angle of the portions and change the random orientations of all the portions at once. How many highlights do you see on average?

By comparing his/her own impression of the highlights with the values of the coefficients, a careful reader may notice that the visual impression suggests that there are a few highlights, while the coefficients hardly exceed unity.

This is due to "inertia" of human vision: visual stimuli do not abruptly decay after the object causing them disappears from the computer screen. If this decay time exceeds the mean interval between successive highlights, we see more highlights than that the screen instantly contains. This feature of human vision is very important when observing scintillation of a diamond.

The authors suppose that if there was no such feature (temporal contrast), the observer would not distinguish scintillation from the general impression of the diamond.

The software operates exactly as before, but the mirror swings slower than in the previous case. How many highlights do you see on average now?

If we continue splitting the mirror in the same way, LRGIA will remain constant and equal to LRGIA0, while the oscillations WLRGIA will become weaker and weaker. At the same time, the expectancy of BR will first reach its maximum, then will start decreasing, and finally will become zero (the authors suppose that the brilliance of a ground-glass surface is zero). This is because the light flux directed towards the observer's eyes will be reduced when the size of the mirror portions is less than 3 mm (starting from the second stage of splitting the mirror). So, unlike the first splitting stage, the brightness of the lamp images decreases as their number increases. In other words, starting from a certain splitting stage, BR decreases due to contrast lowering at constant LRMSU.
Thus, we have shown that the coefficients used at GIA absolutely do not correlate with the BR coefficient defined intuitively. Moreover, in our imaginary experiment these coefficients almost do not change, while BR changes strongly (first increases and then falls down to almost zero). This example illustrates that the WLR coefficient principally differs from the brilliance, and that WLR measurements do not allow one to study the brilliance. This experiment also shows that the LRMSU coefficient does not correlate with the brilliance as well. However, a multiplicative function of the image contrast and the LRMSU coefficient can be used as a good approximation of the brilliance.

The example considered above is not abstract or far-fetched. It describes rather adequately the brilliance phenomenon perceived by a man looking at a diamond. When no dispersion occurs in the diamond (for example, if the illumination is monochromatic), it acts like a plurality of tiny mirrors. Thus, although the split mirror model is quite simple, it allows us to introduce a correct and adequate definition of primary brilliance.

An observer model

The human eye has a pupil whose typical diameter is about 4 mm. This diameter may change, depending on the conditions of illumination. All the light entering the eye passes through the pupil. If the eye looks directly at a light source, the brightness of the source image formed on the retina is independent of the distance between the eye and the source, provided that the size of this image exceeds the effective size of a cluster of visual receptors in the retina. If there is an object, such as a diamond, between the eye and the source, its elementary prisms act as additional diaphragms. As a result, the light passed through such a prism may produce a source image with a considerably reduced brightness. The action of the elementary prisms depends on their size: a large prism almost does not reduce the image brightness, while a very small prism may produce such a dim image that the eye fail to identify it as a separate object.
Accordingly, the following question arises: What are the optimum source size, distances between the objects, and the diamond cut, which make the observer see many bright and colored images of the source? (The brightness corresponds to the brilliance of the diamond, while the coloration corresponds to its fire).

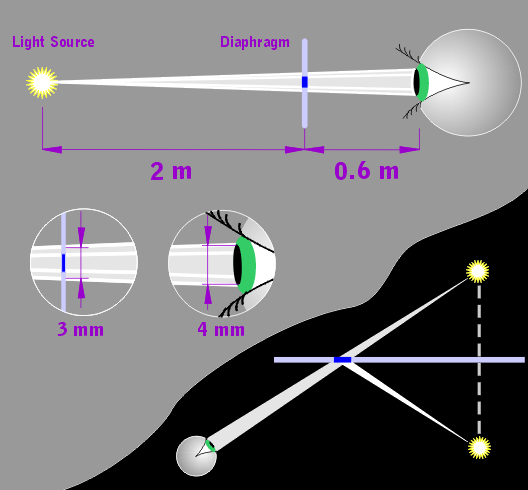
Fig.6. Diamond facet as additional diaphragm for light source

The sizes of the elementary prisms depend on their quantity, the size of the stone, and the arrangement of its facets. Studying this problem allows one to determine the optimum combination of a light source and facet dimensions by numerical calculations. The interrelation between the source, one of the facets, and the eye pupil is illustrated at Fig. 6. In other words, if the light emitted by the source falls on a stone with few large facets, the stone produces few intense light beams; and if the light falls on a stone with many small facets, the stone produces many weak beams. When the number of the facets is large enough, the intensity of each of these beams tends to zero.

It is important to make a diamond grading model adequate not only from the viewpoint of geometrical optics but also from the viewpoint of the psychophysiological features of human perception. When studying the fire, the GIA group uses the following steps:

• Empirical determination of a threshold for the intensity of the minimum signal (page 184 of "Modeling the Appearance…").
• The use of an intensity smoothing function (let me cite a phrase contained on page 183 of "Modeling the Appearance…": "…Thus, rather than use the intensity directly, we "smoothed" it with an "S-shaped" function…" )

We think that at this stage of their studies the GIA group faced the problem of mathematically modeling such phenomena as «subjective brightness» and «subjective size of a highlight». These phenomena are due to the fact that a man perceives light intensity as subjective brightness and subjectively senses the size of a highlight. Some studies on the subjective brightness can be found in literature (section 6.3 «Brightness and Lightness scales», pp. 493-499, in "Color Science. Concepts and Methods, Quantitative Data and Formulae" by G. Wyszecki and W.S. Stiles, 2000).

The GIA group uses the area of a highlight as a measure of its subjective size, while the human brain primarily responds to the linear size of an object.
Of course, these problems have not been completely solved in the literature cited, but the material published there convinces one that the experimental data can be fitted by functions that are essentially different from those used at GIA.

Note: approach used in this article

So far we used a language such as facets, prisms, ray paths, mirrors,
reflections, and so on. This language is useful for understanding and
explaining various phenomena, and many researches uses this language when
analyzing and quantitatively describing these phenomena. However, it is
very difficult to characterize the considered phenomena with maximum adequacy, if using these concepts.

Therefore, researchers introduce some assumptions and simplifications,
consider only selected phenomena, which leads to considerable distortion
(simplification) of the final results. That's why we have chosen another
way and try to analyze the resultant view, as it is seen by the human
eye and perceived by the human brain. And we use software to model all
the objects involved, including the light source, diamond, and observer.

Understanding of brilliance

Below are all the definitions of "Brilliance" that we could find. Secondly we consider why so many definitions exist followed by two definitions of "Brilliance" that match our understanding of this phenomenon.

We would be grateful if you will share your considerations, concerns and comments.

Definitions of "Brilliance":

From Tolkowsky's "Diamond Design", 1919:

The brilliancy or, as it is sometimes termed, the " fire " or the " life " of a gem thus depends entirely upon the play of light in the gem, upon the path of rays of light in the gem. If a gem is so cut or designed that every ray of light passing into it follows the best path possible for producing pleasing effects upon the eye, then the gem is perfectly cut.

Diamonds, E. Bruton (1978):

Eric Bruton F.G.A gives in his book "Diamonds" (1981) definition of brilliance that can be collected from several places of his book: "This quality of returning the maximum amount of light from the stone to the eye - from the surface lustre and from internal reflection - is knows as "life". "The fire of a gem is the display of spectrum colors (and scintillation) caused by its refracting white light before returned to the eye". "Brilliance has never been exactly defined. As it is used in a general way, it should cover all the visual properties which have been concentrated, in the two last paragraphs, into the terms "life" and "fire". .....The brilliance of a stone depends upon the optimum combination of its lifre and fire. If the two qualities could be quantified, brilliance would be at maximum when life X fire was at a maximum".

GIA Diamond Dictionary, 3rd edition:

Intensity of the internal and external reflections of white light from the crown of a polished diamond or other gemstone. Hardness, refractive index, reflectivity, polish, luster, and proportions all affect a gemstone's brilliance.

Diamond Grading ABC by V. Pagel-Theisen, 11th edition:

External brilliance - luster, produced by reflection of light on the surface of the facets; Internal brilliance - refraction and total reflection of light on the pavilion facets; Dispersive brilliance - splitting of scattering of light into its spectral colors = the dispersion which evokes the "fire" or "life" in a brilliant; Scintillation brilliance - the "sparkle" of the stone when moved, caused by light reflections of the light source.

Dodson's definition (1978):

A measure of the light that, entering the crown of the stone, is scattered out of the crown facets.

"Professional Jeweler" (July 1998) Light Return/Brilliance:

The amount of light returned to the eye, or brilliance, depends on how well the diamond in question reflects and refracts light. This includes dispersed wavelengths, which are reflected from the internal surfaces of a diamond and returned to the eye.

GIA (G&G Fall 1998):

White light returned through the crown (excluding glare - light directly reflected from the top surface).

Garry Holloway: http://www.diamond-cut.com.au/09_brill.htm

Brilliance is the human perception of diamond brightness. It is the most important feature of a beautiful diamond.

Brilliance is not simply light return, it involves complex issues that include scintillation or contrast with the added variable of human perception. However a diamond with poor light return cannot display optimal beauty.

Discussion

Today diamond appearance is described by gemologists and those in the trade in terms of Brilliance, Scintillation and Fire. These three terms are commonly accepted as completely describing diamond appearance.

Yet a literature review and comparison of trade opinions show the term "Brilliance" is not clearly defined; there is no one generally accepted definition.

Probably about 50 years ago the word "Brilliance" was used as ultimate description of the diamond appearance. At that time it was a synonymous with "Beauty". An evolution occurred that led to the term "life" to be deleted from the commonly used terms and the term "Scintillation" became commonly associated with the effect of a moving diamond. Fire too has become clearly separated as a characteristic of the colored component of Brilliance.

As you can see there are many different definitions for brilliance in a diamond.

At present time there are three different ideas of brilliance:

• Diamond beauty (Life) (as 50 years ago);
• Diamond beauty minus Scintillation minus Fire;
• Light Return (sometimes including external luster or sometimes taking

Our definitions of "Brilliance" for your consideration:

First definition :

Brilliance is the characteristic of a diamond, which remains when we "take" all its appearance and "subtract" Scintillation and Fire. The human eye will see Brilliance as combination of white, gray and black zones for motionless diamond ( i.e. colored zones are eliminated).

Second definition :

The phenomenon called Brilliance consists of two parts. The first one is based on comprehension of primary/initial/incipient brightness and contrast of diamond image (motionless photo-shots taken from different positions), and this part can be called "primary approach". The second part consists of posterior/subsequent traditional comprehension of some phenomena in diamond. HUMANS seek to DEFINE WHAT WE OBSERVE AS SIMPLIFIED AND UNDERSTANDABLE CONCEPTS. THIS LED US TO ATTACHING CONCEPTUAL LABELS based on phenomena that are currently described and viewed as being negative or positive (like «Fish-Eye», «Nail Head», «Leakage», thick girdle, symmetry deviations, Tolkowsky pattern, «Ideal Cut» etc.). This can be called "the expert approach".

This "expert approach" evolved after attempts to grade the characteristics used to describe brilliance and to interpret it by viewing many diamonds. Professionals in the contemporary market have established in their minds standard images which are labeled and associated with positive or negative values that evoke specific tastes and emotions.

The equivalent expertise is however are quite rare among the general diamond buying populace. What is even more disconcerting is that those with the greatest diamond experience and expertise generally examine suet diamonds in flood 'office' lighting because it is difficult to grade the clarity of a diamond in the same environment that diamonds are commonly purchased in by consumers. This situation is exacerbated by the fact that it is common for trade 'experts' to carry out a complete assessment of a diamond based on its appearance as seen through a loupe in this flood and back lit dealer environment.

Perhaps to evaluate Brilliance objectively the "primary approach" would be adequate, but it would not be enough for a human subjective evaluation because a human mind could hardly grade/calibrate it even if the correct assessment method for end consumers was used. It is easier for a human brain to grade/evaluate Fire or Scintillation because under fixed illumination conditions one can easily count "two flashes" or "four bright sparkles during motion". More recent attempts to replace "Brilliance" by "Light Return" is bound up with the very need to provide a quantitative grade.

Comprehension of the first part of Brilliance depends on sex and age of people. Comprehension of the second part of Brilliance depends on the environment/culture where people grow. A person develops an ability to evaluate the quality of wine under the influence of different social factors like advertisements, expert opinions, friends advice, etc., even if he thought he tastes vine by himself. The appreciation of brilliance has similar tendencies. These activities are motivated by the same reason: people wish to join an elite social group. As a consequence the comprehension of the second part of Brilliance will vary for different nations, times, social groups, etc. Vine is only one example and other examples can be preferences of clothes, women, men, pets, cars, books .... etc.). Here it is important to note that a person can choose vine among all vines what society offers to him. He can not choose a vine what is not available today, or in his socium. This is important selection and it defines regional preferences for example.

Practical value of the cut grading system

It is important to develop a diamond grading system capable of objectively grading diamonds on the basis of their appearance and beauty, that is, entities seen by the eye and perceived by the brain. The grading system is a tool that can be used to solve a number of practical problems, such as, grading fancy cuts, developing and grading new cut styles (automated scanning of parameters), certification, branding (production of branded articles and development of instrumentation for its identification), internet shopping.

Besides the practical value, any technology has its limits of validity. Nowadays, scanning systems (manufactured by Sarin) have certain accuracy. This limits the capabilities of quantitative and qualitative analysis of diamond cut, which can be performed. Diamonds graded by sight as super-symmetric cannot be distinguished from just well-cut diamonds. The classical distortions of symmetry classified as «Minor symmetry» at GIA cannot be at all analyzed on the basis of scanned models. We think that starting from a certain magnitude, the symmetry distortions will be so weak that they will not affect the appearance of the diamond, though during certification at GIA these distortions might be noticed and classified as «Minor symmetry». As an example, Eightstar stones can be reminded that are symmetric for the observer, are symmetric according to a Firescope, but not always get the Excellent symmetry rating from GIA. We believe that the present level of technology allows one to produce an inexpensive commercial scanner and corresponding software, which would build a diamond model with accuracy required to correctly analyze the appearance of the diamond. To achieve the best price/quality ratio it is necessary to combine two technologies: projection-scanning and independent diamond facet junction building topology.

Acknowledgment 

We with to thank the following people without who our diamond cut studies would be absolutely impossible: Alexander Shevchenko (OctoNus, Russia), Olga Ohrimenko (Russia), Sergey Savrasov (MSU, Russia), Anton Vasiliev (Lal company, Russia), Bruce Harding (US), Michael Cowing (US), Leonid Tcharnyi (www.pricescope.com  , Canada), Paul Van der Steen (DiamCad, Belgium), Michail Sherbakov (Alrosa, Russia), Eugenia Kyznetsova (MSU, Russia), Ilja Nikolaev (MSU, Russia), as well as active participants of discussions on diamond cut, which took place at the DiamondTalk.com forum. We wish to express special thanks to the group of diamond cut researchers from GIA and our other opponents who inspired us to deeply study the problems of diamond cut.

PS. Further development of these studies requires collaboration of specialists representing different areas of expertise. This is because the diamond cut studies are at the interface of many traditional sciences. Ray tracing is based on optics, physiology and psychology study the features of human vision and perception, respectively, computer modeling helps to make the diamond cut studies less expensive, marketing research is needed for practical applications, while gemology studies the diamond itself. That's why we are looking for colleagues and like-minded persons.

Efforts of researchers from different countries are now forming a new trend in gemology, which incorporates optical knowledge and modern methods of modeling. Our activities involve writing papers, creating web-sites, visiting web forums, and discussing various problems with colleagues and opponents. All these activities help to develop this new trend. We would like to intensify the exchange of knowledge between other parties interested in the problem and ourselves, because we consider this important for creating, developing, and disseminating new knowledge.

References

1. Apenko M.I., Dubovik A.S. (1982) Applied Optics. Moscow, 352 pp. In Russian.

2. Born M., Wolf E. (1964). Principles of Optics. Pergamon Press.

3. Bruton E. (1981). Diamonds. Revised and reprinted edition, N.A.G. Press Ltd., London, pp. 226-227.

4. DODSON J.S. (1978). A statistical assessment of brilliance and fire for the round brilliant cut diamond. OPTICA ACTA, v.25, N.8, p.681-692 .

5. Fedotov N.T. (1939). General color science. State publishing house for science and technology, Moscow, 228 pages. In Russian.

6. Glassner A.S. (1995). Principles of Digital Image Synthesis. Vol. 1. Morgan Kaufmann Publishers, Inc., San Francisco, Ca. 540 pp.

7. Hemphill T.S., Reinitz I.M., Johnson M.L., Shigley J.E. (1998) Modeling the Appearance of the Round Brilliant Cut Diamond: An Analysis of Brilliance. Gems&Gemology, Fall 1998, Vol. XXXIV, No. 3, pp. 158-183.

8. Holloway G. (2001). Defining the Beauty and Desirability of Round Brilliant Diamonds. http://www.diamond-cut.com.au/09_brill.htm

9. Hubel D.H. (1988) Eye, Brain and Vision. Scientific American Library, A division of HPHLP, New York.

10. Judd D.B., Wyszecki G. (1975). Color in Business, Science and Industry. John Wiley&Sons, New York.

11. Liddicoat R.T. (Ed). (1993). The Diamond Dictionary. Third Edition, GIA, p. 28.

12. Lipson S.G., Lipson H., Tannhauser D.S. (1995). Optical Physics. Cambridge, University Press, 1995.

13. Novakovsky S.V. (1997). Color on a TV screen. Basics of television colorimetry, Moscow, Radio and communication. 168 pages. In Russian.

14. Pagel-Theisen V. (1993). Diamond Grading ABC. Handbook for Diamond Grading. 11th Edition, pp. 153 - 162.

15. Pribram K.H. (1975). Languages of the Brain. Moscow, Progress, 463 pp.

16. Reinitz I.M., Johnson M.L., Hemphill T.S., Gilbertson A.M., Guerts R.H., Green B.D., Shigley J.E. Modeling the Appearance of the Round Brilliant Cut Diamond: An Analysis of Fire, and More About Brilliance. Gems&Gemology, Vol. XXXVII, Fall 2001, pp. 174-197.

17. Sivovolenko S.B., Shelementiev Y.B., Vasiliev A.V. (1999). The results of diamond cut studies carried out in Moscow State University. https://octonus.com/projects/diamond-cut-study/diamond-cut-studies-results

18. Sivovolenko S.B., Shelementiev Y.B., Vasiliev A.V. (1999). Determination of the cut quality of a diamond and visual evaluation of its beauty. https://octonus.com/projects/diamond-cut-study/determination-of-the-cut-quality

19. Sivovolenko S.B., Shelementiev Y.B. (2000). Developing of Diamond Cut Grading System by MSU (OctoNus and GC MSU) Computer Tools. https://octonus.com/projects/diamond-cut-study/diamond-cut-grading-system-octonus

20. Sharonov V.V. (1961). Light and color. State publishing house of physical and mathematical literature, Moscow, 311 pages. In Russian.

21. Tolkowsky M. (1919). Diamond Design. E & F.N. Spon, Ltd., London.

22. Vasiliev A. V., Rainbow in Colorless Gemstone., 1995, Acta Universitatis Wratislaviensis No 1607, Prace geologiczno-mineralogiczne XLIV, p.147. In Polish. https://octonus.com/projects/diamond-cut-study/rainbow-colorless-gem

23. Wyszecki G. Stiles W.S. (2000). Color Science. Concepts and Methods, Quantitative Data and Formulae // Brightness and Lightness scales, pp. 493-499.