Selection of Facet Slopes

Any gem cutter faced the problem of defining the angles between the facets of a gem being cut. The importance of the proper choice is proven, for example, by the fact that when Marcel Tolkowsky published in 1919 the "ideal" diamond cut proportions he had invented [1], many people re-cut their diamonds in spite of the inevitable loss of weight. The reason was much better appearance of the diamonds that were cut in accordance with the proposed rules. The price of a diamond of a non-standard shape is still determined by the size of an ideal-cut diamond that could be made of the diamond evaluated. Since those times, a lot of various sets of facet slopes and methods of their calculation have been proposed [2-5].

It is notable that the number of papers dealing with the optical properties of a cut gem greatly increased recently [6-15]. If one tries to summarize all the recommendations made by different authors, he may get confused. These recommendations often not agree with one another, sometimes they contradict. This discrepancy may be due to the fact that each author is so keen on his own solution, which follows from the initial suppositions he has chosen, that he doesn't notice many other aspects of the problem. It is also confusing that the beauty of a cut jewel depends on a number of factors that do not have accepted terms. In spite of the subjectivity of the concept of beauty itself, we'll try to objectively consider from various points of view how the optical properties of a jewel depend on the angles between its facets and to justify the ranges of their variation, which should not be violated, if possible.

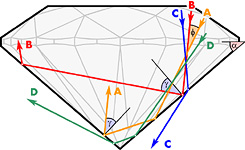
The main purpose of a faceted gem considered as an optical element is to reflect towards the observer's eye as large portion of the incident light as possible. Modern cut styles achieve this due to double total internal reflection at pavilion facets (the bottom of the gem). Let us trace the rays shown in Fig, which pass thru two opposite pavilion facets that make the angle a (pink sector) with the girdle plane of the gem. The conditions of total internal reflection are met at both facets only for those rays having a direction of incidence that is within the angle f (yellow sector).

(Note that here we consider the angle inside the gem; the corresponding angle in the air is differ due to refraction.)

For the ray 'С' the total internal reflection is violated at the first facet, while for the ray 'D' this occurs at the second facet. The range of all possible directions of the incident rays that meet the conditions of total internal reflection can be determined analytically:

f = 180 - 2g - 2a

where g = arcsin (1/n) - the critical angle of total internal reflection for a given material with the refractive index n.
It follows from the above expression that a decrease in a results in an increase in such parameters as f, the number of incident rays that return back, the probability of observing these, and, finally, the brilliance (or more strict - light return coefficient) of the jewel. It is especially useful to decrease the slope angles of bottom facets for heavily colored samples, because this decreases the path of a ray inside the gem, preventing the ray coloration due to absorption spectra.