A statistical assessment of brilliance and fire for the round brilliant cut diamond

Abstract

The 58-facet round brilliant cut diamond is considered as a random scatterer of incident light. The diamond, of an axisymmetric design, is considered to be spinning and surrounded by a hypothetical sphere. The optical properties brilliance, sparkliness and fire are presented by statistical properties of the intensity distribution on the sphere. Using a computer model of the system, the effects on the three optical properties of changing the length of the pavilion halves and the table spread were investigated. The results confirmed that the traditional 'ideal' cuts are satisfactory, showing the trade-off between sparkliness and fire that results with these ideal cuts. A new style is proposed with a deeper pavilion angle (53°), and this is shown to be superior to the traditional styles using the statistical measures.

Historical survey

Fig 1. The old mine cut style after Tolkowsky [1].

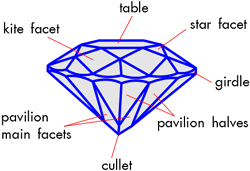
Diamond has been valued as a talisman since ancient times, but only since the 17th century, and the styles associated with Cardinal Mazarin and Peruzzi has cutting to produce a pleasing optical effect become popular. A stage in the development of the point cut into what now is called the round brilliant cut diamond, by trial-and-error methods aided by serendipity, was the 'old mine cut' style (see figure 1), popular at the turn of this century. This style, with its high crown, steep pavilion and recognizable arrangement of facets, exhibits the three prized effects in a gemstone - brilliance, a measure of the light that, entering the crown of the stone, is scattered out of the crown facets, sparkliness, the amount by which this light sparkles, and fire, the chromatic variation of the sparkles. These visual effects are still quantified by reference to experienced judgement, there being no engine available to measure all three parameters.

With the fashion for mathematical determinaism in Victorian science, which carried over into the 20th century, it was inevitable that a mathematical description of the optical effects in a polished diamond should be sought. It was in 1919, when the technical optics section at Imperial College was 'one and just begun', that Tolkowsky published a book, "Diamond Design" [1], while a member of the city and Guilds College (now the engineering school of Imperial College). This theoretical monograph was the first attempt to list the causes of the optical effects in gem diamond and set some simple criteria for their measurement.

Fig.2. The 'ideal' proportions proposed by Tolkowsky [1].

Taking as his starting point a simple triangular cross-section, he used geometric and optical arguments to justify the necessity for, number of and arrangement of the facets on the centrosymmetric round brilliant cut diamond that was the old mine cut, and hence to confirm this as the ideal style for cutting a gem diamond by defining a criterion for maximum brilliance. This stated that the optical goodness of a stone is the product of the angular dispersion for a red and blue ray and the transmitted intensity for a green ray at the same angle of incidence. However, in the derivation of the functional form of this product, [1, p.72] he appears to have confused Lambert's law with Fresnel's equations, and hence fortuitously deduces the ideal pavilion angle to be 40 3/4°. If the brilliance criterion is calculated using the exact formulae, but otherwise following the analysis of Tolkowsky, an ideal pavilion angle of about 39 1/4° is found. It is to be noted that Tolkowsky's ideal proportions (see figure 2) are accepted by the Gemmological Association of America as the best of the 'ideal' proportions proposed up to the present time.

In 1926, Johnsen [2] used similar geometric methods to obtain another ideal set of proportions. These had a pavilion angle of about 39°, similar to the more exact analysis of Tolkowsky. In the same year, Rosch [3] published a set of ideal proportions and also developed a technique for producing, for a gem diamond, a reflection spot picture, the light analogue of the X-ray back-scattered Lauegram. These spot diagrams can be used to aid identification and to assess the optical goodness of the gem.

One prevalent argument at the time was that these optically 'ideal' cuts were less economic than the mine cut since more material was removed, resulting in a lower yield from the rough. Because extra material had to be removed, and a higher accuracy and standard of workmanship were demanded, the stones took longer to manufacture and so the new styles were slow to be adopted. The final value of a stone depends on the 'four-Cs' - cut, clarity (the freedom from both internal imperfections and artefactual blemishes) and carat weight (1 carat = 200 mg). By appraising many stones, Eppler [4] produced in the 1930s a set of practical cuts which helped to combat the resistance to the new styles of cutting.

In a paper which appeared in 1968, Eulitz [4] adopted a geometrical approach similar to that of Tolkowsky and Johnsen. Elbe [6,7] has also produced some designs for a new type of round brilliant, as well as a diamond grading engine based on the methods of Rosch. Most recently, Stern [8] has developed a computer programme that uses finite ray-tracing methods, and had confirmed that the traditional ideal cuts are satisfactory. He fails, however, to discuss any quantitative measures of optical goodness, proposing only a loose criterion for optical quality that is a restatement of a well-known preference; this will be given in the next section.

Factors affecting optical goodness

The non-expert normally observes a diamond set into jewelry with the pavilion obscured by the setting in diffuse illumination, with the unaided eye, and at a distance of about 50 cm (a relaxed arm's length). The observer moves both his head and the stone, and the overall brightness, ray of sparkle and chromatic variations in the sparkles are transferred into degrees of optical attractiveness. It would appear that, when he judges optical attractiveness, the observer has in mind certain general principals and some specific likes and dislikes. In particular the illumination over the stone should be reasonably uniform, and there are two styles which offend this rule in the round brilliant cut. One is a stone with a deep pavilion (pavilion angle ~ 45°), which gives the impression of a dark table, which is not surprising since the table-pavilion combination is like a corner-cube retro-reflector with the observer's head forming a dark central obstruction. The other is a stone with a shallow pavilion angle (of 37° or less) where the girdle, which often has a brutted or frosted appearance, is visible through the table as a white ring. In general terms, the grater the number and the smaller the average size of the sparkles, the more evenly will they be distributed. If this situation were to be modelled in every detail by a computer programme, it has been estimated that three hour's computing time would be required to perform the ray tracing alone, before any analysis of the data would be possible. A refinement of the Rosch's method [3] was therefore adopted.

The diamond grading model

A diamond is surrounded by a hypothetical sphere centred on the table; rays in several azimuthal and meridional orientations, a form of pseudo-diffuse illumination, are then traced through the diamond, noting their Fresnel components at each partial transmission or total internal reflection, for it is necessary to know both the intensity and direction of the rays. The final positions on the sphere of rays scattered out of the prism are then calculated, and since the intensities of the spots at those points are known, a map of intensity can be built up for a given sphere radius and a particular refractive index. By tracing at different refractive indices, the various colours can be modelled. In using this technique, one piece of information is lost: the position on the stone from which the light came. Thus it is not possible to directly take account of the visible girdle or dark table effects on this approximation. The resultant spot pattern for a good diamond is a random scatter of points in the whole of the forward hemisphere, and some property of this randomness is required as the measure of optical goodness.

The overall brightness is relatively easy to define :

Forward brilliance = Intensity scattered into forward direction / Total illumination

But how are sparkliness and chromatic variation to be measured? Two authors have given the analysis of spot pattern some consideration. Elbe [7] used a photometer to measure the intensity distribution of a diamond, the stone being rotated while a radial scan of the intensity distribution was made. In the resultant distribution, the total number of sparkles was taken as the measure of optical goodness. Stern [8] modelled the 'gemprint' of Bar-Isaacs, which used the same technique as Rosch and Elbe except that a laser light source, in which a lens brings the far-field diffraction pattern to a convenient image plane, is used. Stern's criterion was that the far-field diffraction case of the well-established criterion that an even distribution of sparkles is preferred. No chromatic effects could be measured because of the laser illumination. Elbe's criterion, based on a count of sparkles, also only partly fulfils the requirements of a visual grading measure for diamond; again no criterion for chromatic variation was given. However, Elbe's simplification of the two-dimensional intensity distribution to a one-dimensional intensity scan, coupled with a technology that enables scans for several wavelengths to be made, yields a technique and data base that are suitable for further analysis.

The analysis of random signals has led to ideas of correlation analysis. The thesis of this paper is that the intensity scan produced by a gem diamond can be considered and analysed as a random signal. In particular, the two questions, how sparkly and how fiery a diamond is, are asked in terms of probability theory in the following way: how different in intensity is each point in the distribution of light from each other point, and how different is the distribution in red light from those in green and blue? The answers are obtained by auto-correlating the intensity distribution and cross-correlating say, the red and blue intensity scans. In our case, we require an even distribution of sparkles and a measure of their average size, which is given by the half-width of the auto-correlation.
In one dimension the auto-correlation of a constant is another constant, but that of a far-field speckle pattern from many diffusing element has the well-known gaussian form. For a diamond, these would correspond respectively to no sparkliness, the worst case, and to an even distribution of sparkles.
A suitable measure for sparkliness would therefore be how far the auto-correlation deviates from a constant; the higher the deviation, the better, in a sparkling sense, for the diamond. Such a possible measure is the variance of a distribution,

which enables a sparkliness criterion to be defined as the valiance of the auto-correlation of the total radial intensity scan, where, as done by Elbe, the diamond is rotated, and for a particular azimuth with respect to the table normal all the intensity spots are sampled, whatever meridional angle they subtend. Concerning the fire, the intensity distribution is calculated for wavelengths in the red, green and blue regions of the spectrum. An argument similar to that used for sparkliness is proposed, the variance of the cross-correlation would yield the same results as would the auto-correlation. That is, if

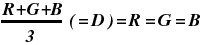
then

which implies white sparkles. Hence the proposal for a measure of fire is that it is the quotient of the variance of the cross-section for the red and blue intensity scans and the variance of the auto-correlation of the total intensity distribution.
We now have a measure for brilliance, sparkliness and fire. Some might prefer a more simple, single figure for the optical goodness of a gem diamond, instead of a triplet. One method of assigning a single figure to each point in the intensity distribution is to assign colour-coordinates to the elemental areas, i.e.

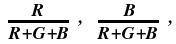
and then from a colour-difference coordinate for each point

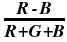
The variation of this factor, which we can call the differential chroma, could then be used as a simple measure of fire. Similarly for sparkliness, we could take the variation of the intensity distribution. However, sith the forward brilliance three factors are again required to fully describe the round brilliant cut diamond, and so it would be naпve to expect a single quantity to describe the optical goodness of such a complex effect.

The computer program

A computer programme was written to incorporate details of the model and calculate the statistical measures outlined above.

It can be split into three major units: the calculation of the shape of the prism, the ray-tracing through the prism, and the statistical analysis of the resultant spot pattern; a schematic diagram of these main elements is given in figure 3.

Fig. 3. The basic structure of the computer program

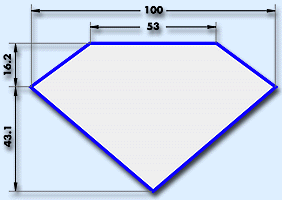
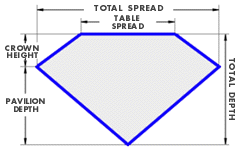
The calculation involved in finding the direction cosines of the normals for the planes that define the prism can be greatly reduced by exploiting the eight-fold rotational and mirror symmetry of the round brilliant cut (see figure 4), this resulting solid (see figure 5) having only eight bounding planes. Then by requiring that the table when, viewed perpendicularly, should form with the stars two interlocking squares, it is possible to describe the prism in terms of six factors. These are the total spread, the table spread, the crown height, the pavilion depth, the total depth and the pavilion half-factor (PHF), the fraction by which the pavilion halves extend towards the collet from the girdle (see figure 6).

Fig. 4. The proportions for the round brilliant cut diamond.	Fig. 6. The proportions for the round brilliant cut diamond.	Fig. 5. The generating solid for the round brilliant cut. The plane labelled a is the false plane.

The ray-tracing section has three subdivisions. The first traces the input rays to the surface of the prism, the second traces the rays, using vector ray tracing equations, through the prism, and the third traces rays scattered out of the prism onto the hypothetical sphere. The false planes of symmetry (see figure 5) have special optical properties; the fresnel equations are not applied, as the planes are only a mathematical device, and all rays are simply reflected, whatever their angle of incidence. Finally, the statistical package calculates the measures for brilliance, sparkliness and fire, both the auto-correlation and cross-correlation being approximated by a serial product, i.e. for a function Q (x) the serial form is

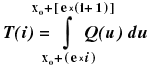
For two functions, say T(I) and S(I), the serial product is

This package also contains routines for producing graphical output on the systems in use at the Imperial College Computer Centre.

The effect of the pavilion half-factor

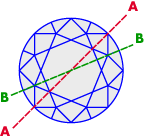
Of the many approximate calculations that have been made of brilliance and fire, only one has used a three-dimensional model, and of the two-dimensional models many have considered only the classic diamond cross-section A-A in (figure 7). It has been argued that the table, kites and pavilion mains are the principal facets, and that the stars and halves play only a secondary role in optical effectiveness.

Fig. 7. The round brilliant cut diamond showing the classic cross-section (A-A) and a more complex cross-section (B-B).

Historically, the fashion was to polish the table to about 40 per cent of the diameter of the stone and to have short pavilion halves, and for such cuts the argument about principal and secondary facets was probably valid. Recently, however, especially in Europe, the fashion has been to polish the table to up to 65 per cent of the total spread and the pavilion halves have an area greater than the pavilion mains, and the two-dimensional cross-section (such as B-B in figure 7). This can only, at best, be considered a first approximation as the normals to the facets for these cross-sections do not lie in the same plane. Hence the three-dimensional character of the prism must be considered. The programme was used to investigate the effect of changing the PHF for a round brilliant cut diamond with a crown height of 15 per cent and a table spread of 50 per cent, a style not dissimilar to that of Tolkowsky [1]. In addition, the pavilion angle is restricted to between 37° and 45°, the range into which all so-called 'good' brilliants fall The results are presented in figures 8 to 13.

Fig. 8. The effect on brilliance of a change in PHF.	Fig. 9. The effect on the variance of the intensity distribution of a change in PHF.
Fig.10. The effect on the sparkliness of a change in PHF.	Fig.11. The effect on the differential chroma of a change in PHF.
Fig.12. The effect on the variance of the cross-correlation of a change in PHF.	Fig.13. The effect on fire of a change in PHF.

Discussion of the effect of the pavilion half-factor

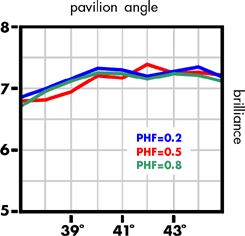
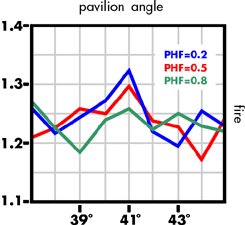
The forward brilliance is fairy constant over the range of pavilion angles, and equal for all the PHFs), thus confirming that forward brilliance alone is no guide to the optical goodness of a diamond.

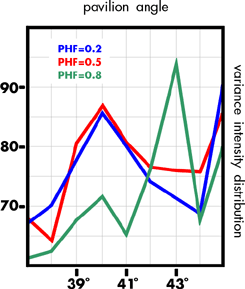
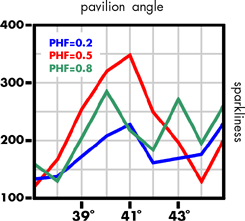
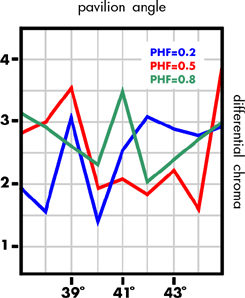
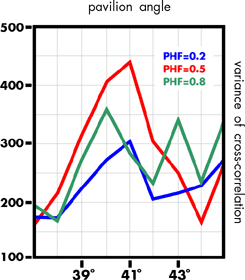
Considering first the variance of the intensity distribution, all PHFs have a peak value for a 40° pavilion with PHF 0.8 and 0.2, peaking again at 43° and 45°; ideal pavilion angle being 41°, PHF 0.8 and 0.5 peak at 39° in accord with Tolkowsky exact and Johnsen while the differential chroma increases again for pavilion angle 45° independent of PHF.

Considering the measure for sparkliness, both PHF 0.2 and 0.5 peak at pavilion 41° and PHF 0.8 peaks at 40° with 0.5 max > 0.8 max>0.2 max. Again the sparkliness increases for all the preferred pavilion angle. The measure of fire gives a less confused result than the differential chroma: all PHFs peak at a 41° pavilion with the PHF 0.815 per cent greater than PHF 0.5.

As the normal practice is to keep the pavilion angle between 39° and 42°, and as it is possible to gain a higher yield from a piece of rough diamond with a lower pavilion angle, the shallow pavilion style is often encountered. For a pavilion 39°, PHF 0.5 still shows more sparkliness than either PHF 0.2 and 0.8. However, the fire factor of PHF 0.8 is 45 per cent higher than PHF 0.5. Thus the effect of the economics of production is acceptable to the current fashion.

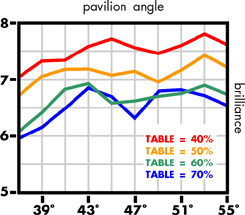
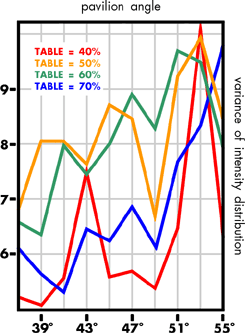
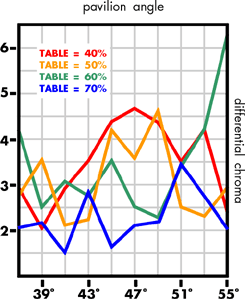
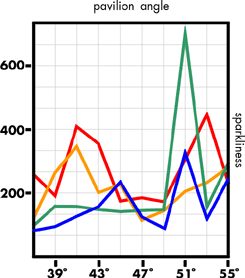
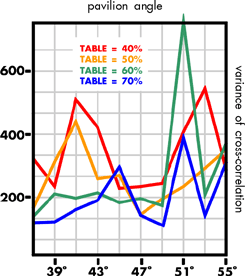
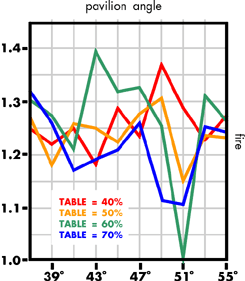
The effect of varying the table spread

Let us now consider the other current fashion, that of polishing the table to up to 65 per cent of the total spread, bearing in mind that the 'ideal' table diameter is 50-55 per cent of total diameter, and that the earlier preference with the old mine style was for 40 per cent table spreads. Recall also that Elbe has produced a design for a brilliant that has a pavilion angle outside the range 39°-42°, and that several other authors have also produced designs with un-orthodox proportions and facet arrangements. The programme was used to investigate pavilion angles of from 37° to 55°, virtually the angle of the octahedral face, a typical 'habit' for rough diamond, the PHF being held at 0.5. The results are presented in figures 14-19.

Fig.14. The effect on brilliance of a change in table spread	Fig. 15. The effect on the variance of intensity of a change in table spread
Fig.16. The effect on the differentiation chroma of a change in table spread	Fig.17. The effect on the sparkliness of a change in table spread
Fig.18. The effect on the variance of the cross-correlation of a change in table spread	Fig.19. The effect on the fire of a change in table spread

Discussion of the effect of changing the table spread

The brilliance falls off with increasing table spread, exhibiting progressively two sets of peaks centred on pavilion angles of 41°-43° and 51°-53°. Again, the simpler measures of sparkliness and fire are confused, both having many peak values in the pavilion angle 37°-55°. The results for the two statistical measures of brilliance and fire are again less confused. The double peak seen for the brilliance appears again for the sparkliness. The 40, 50 and 0 per cent table designs peak at pavilion angle 41°, the 70 per cent design at pavilion 45°, the second set of peak values occurring at pavilion 51° for the 60 and 70 per cent tables and 53° for the 40 and 50 per cent tables.

In terms of fire, the 40 and 50 per cent tables still peak at a 41° pavilion angle. While the 60 and 70 per cent tables are falling at 41° pavilion, being lower by 50 per cent over the preferred pavilion range 39-42°, the position is reversed, these table spreads having, at 39°, a value higher by 55 per cent than the 50 and 40 per cent table spreads.

We can invoke the previous argument that 39° pavilions are as acceptable as 41° pavilions, and that the lower sparkliness can be compensated by an increased chromatic effect without detriment to the stone's optical goodness; the modern practice of large tables and long pavilion halves can then be accounted for in some measure by economic expediency influencing a caprice (more fire, less sparkle) of fashion, another popular belief being that a stone with a larger table looks bigger for the same diameter.

The statistical measures for sparkliness and fire confirm the traditional ideal proportions are correct; they also help to reconcile the differences between the sets of ideal proportions by showing the increase in sparkliness and loss in fire for the PHF 0.5 41° pavilion against the PHF 0.8 39° pavilion. This helps to establish a scale of optical goodness but no definite conclusion can yet be drawn as to how much greater sparkliness is valued above fire, or vice versa. It is, however, tentatively suggested that brilliance and sparkliness are the two most important factors.

A proposed new cut

The multiple peaks in the sparkliness and fire factors lead to the conclusion that the traditional design for the round brilliant cut diamond is not the only solution. It is proposed that a design with a table spread of between 40 and 50 per cent, crown height of 15 per cent of the total spread, a pavilion angle of 53° and pavilion half-factor of 0.5 would look as attractive, if not more so, than a stone of similar diameter in the traditional preferred proportions.

Acknowledgments

I would like to thank Professor W.T. Welford for his encouragement during the course of the project and useful discussions concerning this paper. I am also indebted to the Diamond Trading Company (Pty) Ltd. for supporting the project, and their Executive Committee for permission to publish this paper.